こんにちは今日もコロナ社から出版されている自然言語シリーズの自然言語のための機械学習入門を読んでみました.クラスタリングは文章の性質の違いを明確にするために使われることがあるようです.
はじめに
クラスタリングはデータを似た者同士で分けることです.分類との違いはわける数(クラスタ数)が決まっていない点です.データの性質の違いでクラスタリングができれば,その性質によって異なる処理を効率的に行うことが可能となります.クラスタリングの種類としては「凝集型クラスタリング」「k-平均法」「混合正規分布」などがあります.また,混合正規分布などはEMアルゴリズムという枠組みの一部です.
凝集型クラスタリング
データがある空間に分布しているとき,個々のデータ間の関係から階層関係を作り出すクラスタリングです.データが徐々にまとまっていくことからボトムアップクラスタリングとも呼ばれています.概念図を以下に示します.
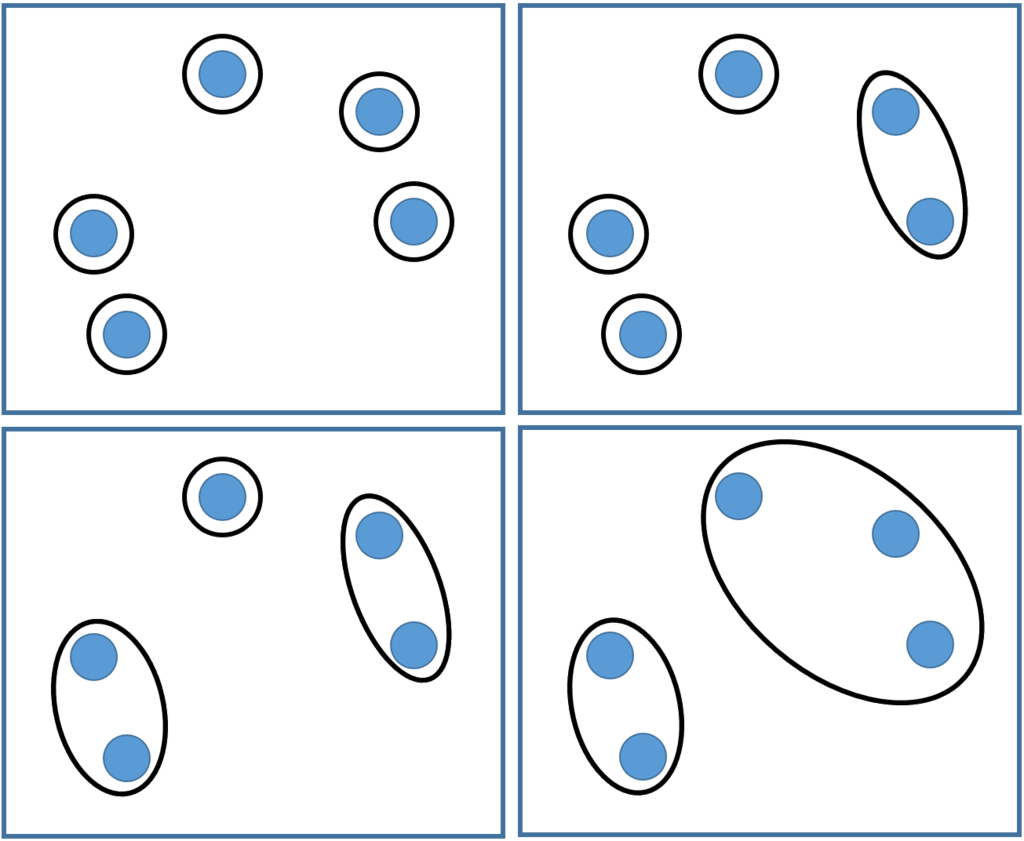
”近いもの”を併合していき,併合の回数を階層数とした木構造を作り出します.併合の回数を任意にすることでクラスタリング数を管理することができます.
この”近いもの”はデータ間の距離になっています.データは併合が進む毎に集合となっていきます.そして,この集合通しの併合の仕方(集合の類似度関数)がいくつか定義されています.
- 単連結法
集合の各データどうしの類似度で最も大きいものを集合の類似度とします.
- 完全連結法
集合の各データどうしの類似度で最も小さいものを集合の類似度とします.
- 重心法
集合の各データの平均の類似度を集合の類似度とします.
凝集型クラスタリングでは,集合どうしの類似度が最も大きいものから合体していくため,単連結法では鎖状に伸びる傾向があり,完全連結法では円状に大きくなる傾向があります.これら方法はタスクによって使い分けることが重要となります.
k-平均法
ラスタリング数を任意で決め,適当にデータをわけ,徐々に良いクラスタリングを行っていく方法です.各クラスタは平均ベクトルを持っていて,二段階のクラスタリングを繰り返し行っていきます.一段階目では,データは最も類似した平均ベクトルをもつクラスタに所属します.二段階目では,クラスタの平均ベクトルをクラスタ内データの平均として計算します.これを収束するまで繰り返すことでクラスタリングをおこなっていきます.k-平均法はよく使われるアルゴリズムですが,クラスタ数は固定なので適切なクラスタ数の選択が必要になります.
混合正規分布
k-平均法では,データはどれかのクラスタに必ず属していました.しかし,80%はクラスタ1で20%はクラスタ2という場合もあると思います.これを実現するために各クラスタを正規分布で表現しデータはクラスタまでの距離からそのクラスタである確率p(c|x)を持ちます.このP(c|x)はデータxがクラスタcに属している確率を表しており事後確率となり計算が困難になります.そこで,P(x|c)としてクラスタcでのデータxの発生確率(正規分布)を以下のように仮定して
以下のようにベイズの定理から事後確率の変換をおこないます.
データxの生起確率は複数の正規分布からなっており,混合正規分布と呼ばれます.また,今回の例では,分散σは固定であり,クラスタごとの平均ベクトルmcのみ変化するとしています.
次に「各クラスタの平均ベクトル」を算出します.k-平均法では各クラスタ内データの平均を求めていました.混合正規分布を用いる場合は,以下のように,全てのデータの重み付平均を求めることになります.
EMアルゴリズム
k-平均法も混合正規分布もに二段階のクラスタリングを行っていました.混合正規分布を例にとると,確率の計算(正規分布)とパラメータの推定(平均ベクトル)を繰り返していました.このような枠組みをEMアルゴリズムと言います.
もし,データxiが属するクラスタcが分かっていた場合,以下の最尤推定で分布のパラメータ(正規分布の平均や分散など)を求めることができます.
しかし,初めはデータxiの属するクラスタcはわかりません.なので,代わりにすべてのクラスタに対して確率P(c|x)を重みとして以下のように尤度を足し合わせたものを最大化します.
ここで,θ'は事前に計算されたパラメータ(計算始めは初期化される)です.この関数はQ関数と呼ばれ,前のパラメータθ'と今のパラメータθを区別して以下のように定義されます.
このQ関数を最大化するようなθを求めることでクラスタリングを行っていきます.EMアルゴリズムのEステップでは,P(c|x;θ')を計算し,Mステップではこの結果を用いてQ関数を最大にするθを求めていきます.